久しぶりにDQウォークの記事です。前回は2022年6月の記事だったので、実に2年ぶり。この2年という期間はDQけしケシに費やした期間でもあります。DQけしケシがサービス終了した今、これからはDQウォークの記事も頻度を上げていきたいと思います。
この2年間もDQウォークは細々と続けておりまして、こころドロップ確率のデータ収集も継続しておりました。その積み上げによりサンプル数は10000件を超え、そこそこ信頼性のあるデータになってきたような気もします。この記事では、ここまでのドロップ確率検証状況についてまとめます。
調査の途中経過(2024年8月時点)
| 種類 | 確率 | サンプル数 | ||||
|---|---|---|---|---|---|---|
| S | A | B | C | D | ||
| 通常モンスター | 3.22% | 4.80% | 11.79% | 25.48% | 54.70% | 5274 |
| 強敵モンスター | 3.12% | 5.16% | 11.54% | 21.48% | 58.70% | 2695 |
| メガモンスター | 3.56% | 6.95% | 12.85% | 19.97% | 56.67% | 1237 |
| ほこらモンスター | 2.70% | 4.68% | 9.79% | 28.23% | 54.59% | 1665 |
| ギガモンスター | 1.05% | 7.02% | 13.68% | 29.82% | 48.42% | 285 |
| 地図モンスター | 3.77% | 9.43% | 9.43% | 24.53% | 52.83% | 53 |
| その他 | 2.80% | 4.77% | 12.50% | 21.71% | 58.22% | 608 |
今回から、種類にギガモンスターと地図モンスターを追加しました。地図モンスターというのは、黒竜丸やハヌマーンといった宝の地図のボスとして出現するモンスターです。宝の地図では一般モンスターもボスになることがありますが、それは対象に含めていません。宝の地図限定のモンスターのみを集計した結果です。
Sのドロップ率は3%前後に収束してきた印象があります。一方、Dのドロップ率は55%前後といったところでしょうか。自分のデータなので当然自分の体感とも一致するのですが、皆さんはどうでしょうか。
通常モンスターをレア度別に分類すると以下のようになります。
| 種類 | 確率 | サンプル数 | ||||
|---|---|---|---|---|---|---|
| S | A | B | C | D | ||
| とてもよくみかける | 2.91% | 4.44% | 11.71% | 26.04% | 54.90% | 2681 |
| よくみかける | 3.69% | 4.78% | 12.24% | 26.66% | 52.64% | 1193 |
| ときどきみかける | 3.95% | 5.98% | 12.98% | 27.20% | 49.89% | 886 |
| あまりみかけない | 2.65% | 4.23% | 6.35% | 16.40% | 70.37% | 189 |
| めったにみかけない | 2.46% | 4.92% | 10.77% | 17.23% | 64.62% | 325 |
サンプル数の少なさもあってばらつきはありますが、概ね同じような分布になっているように見えます。その中で、「ときどきみかける」はやや高ランクのこころが出やすい傾向があるように思います。これは、「ときどきみかける」には地域限定モンスターやイベント限定モンスターが含まれることが要因になっているかもしれません。限定モンスターは高ランクのこころが出やすい印象もあるので、その影響が出ているのかもしれません。
シミュレーション
さて、ここで問題です。仮にこころのドロップ確率が上記の通りであったとしたとき、Sを1個入手するまでに必要なこころの入手数の期待値はいくつになるでしょうか。
ここでは、例としてメガモンのドロップ率を使って考えてみます。メガモンの場合、メガモンの種類にもよりますが、D3個でC、C4個でB、B4個でA、そしてA5個でSといったレートでグレードアップするものが多いです。従って、Dの価値を1とした場合、Cは3、Bは12、Aは48、Sは240の価値に相当します。こころを入手する度にグレードに応じた価値の分だけ資産が増加し、その値が240以上に到達したらSが1個手に入るという計算になります。
このモデルにおいて、資産価値が240以上に到達するまでに要するこころの個数の期待値を求めたいわけですが、非常に複雑なので厳密に計算することはなかなか難しそうです。そこで、コンピュータを使ったシミュレーションを行ってみることにします。
こころを1つずつランダムに入手していき、Sが生成できるようになるまでに要するこころの個数をXとして、Xの確率分布をシミュレーションしました。1個1個のこころのグレードの確率分布は、ここまでの調査結果の数字をそのまま使い、S=3.56%、A=6.95%、B=12.85%、C=19.97%、D=56.67%としました。試行回数は100000回としました。
結果は以下の通りです。
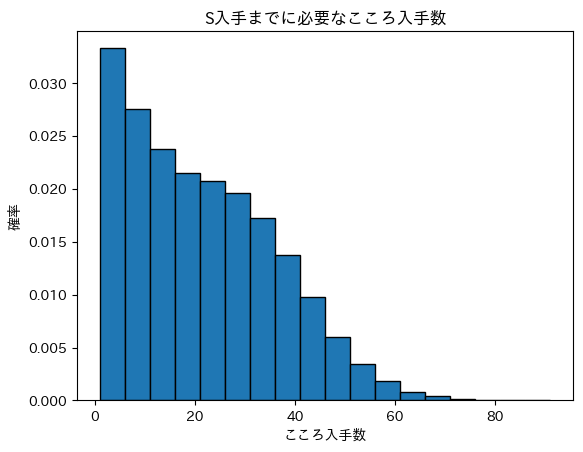
やや意外に思えるかもしれませんが、確率が最も高くなるのはX=1のときです。Sが直ドロップすればその瞬間に終了するので、確率分布としては幾何分布に近く、X=1をピークとした単調減少のグラフになります。Sが直ドロップする事象の確率分布をベースに、A以下を合成してSを生成できる確率が上乗せされているようなイメージです。
このシミュレーション結果において、Xの平均は約21となりました。つまり、メガモンのこころSが1個入手できるまでに必要なこころの数の期待値は約21ということになります。また、99パーセンタイルの値は約59となりました。59個のこころを集めれば、少なくとも1個はこころSが入手できる確率が99%になるということを意味します。
Sが直ドロップするケースと、A以下を合成してSが完成するケースの確率の比もシミュレーション結果から計算してみました。1個目のSが入手できたときに、それがSの直ドロップであった確率は約75%、A以下を合成してSが完成していた確率は約25%となりました。つまり、1個目のSは直ドロップである確率が、A以下を合成して入手する確率の約3倍ということになります。
これらのデータは、皆さんの体感とも一致したでしょうか。もちろん、これらは筆者のデータに基づいたシミュレーション結果ですので、前提が変われば結果も全く変わってきます。あくまでひとつの参考として捉えてもらえればと思います。
にほんブログ村
関連記事&スポンサーリンク




